Part 1. The special theory of relativity
What was wrong with Newtons laws?
To the classical scientist, light was a wave. Waves were well understood by the end of the 19th century. A wave was viewed as a disturbance of the medium carrying the wave. As an example, sound is a wave, the air molecules transmit sound that we hear. The sound wave travels through the air but the air does not move with the sound. The energy of vibration is transmitted from molecule to molecule. It is the rate of this transmission that determines the speed of sound. If you move through air at speed, the speed of sound you measure will depend on the direction. In the direction of your motion through the air, the speed of sound will be lower than if you were stationary in the air. This is because you are catching the sound waves up. All waves seemed to behave this way.
James Clerk Maxwells theory of electricity and magnetism showed that light is an electromagnetic wave. As sound is the transmission of a pressure change, light is the transmission of changes in electric and magnetic fields. Light appeared to behave as a wave and yet it travelled through a vacuum. Because of the wave properties of light, victorian scientists assumed that, as with all other waves, light must be a disturbance of some medium that can transmit the disturbance by passing the energy through the medium. The medium through which light travelled must be some sort of strange electromagnetic stuff that existed in the vacuum of space and was invisible to us. Victorian scientists called this medium the "ether" because of its ethereal nature. Because light appeared to travel in straight lines, even when near observable objects, the ether did not appear to interact with anything else. The ether was considered to be stationary in an absolute sense. The earth should be drifting through this ether. It seemed that a measurement of the difference in light speeds in different directions should determine the motion of the earth through the ether.
The earth goes around the sun at a speed of about one ten thousandth of the speed of light. So the variation in the speed of light in different directions should be at least this figure. In victorian times, direct measurements of the speed of light were not accurate enough to find any such differences. In 1886, Michelson and Morley devised a clever way to measure differences in the speed of light in different directions, by combining the beams together. No such changes in speed were measured even though the experiment was sensitive enough. Other experiments confirmed that the speed of light did not vary. Many theories were concocted to try to explain this. None of these theories worked.
This discovery forms the basis for Einstein's special theory of relativity. He postulated that:
1. No experiment can establish that any frame is at absolute rest.
2. The speed of light is independent of the motion of its source and is the same for all inertial observers.
The speed of light
Just as an aside. When light is not passing through a vacuum it appears to move more slowly. As well as creating relativity theory, Einstein developed some of the fundamental ideas of quantum theory. Quantum theory has a strange view of light called "wave-particle duality". In transparent materials, light packets called photons travel a short way at 299,792,458 m/s and are then absorbed by a molecule in the material. A short time later an identical photon is reemitted. It is the delay between absorbtion and reemission that makes the light beam move slowly. The photons themselves still travel at the proper speed. This has nothing to do with relativity theory. I just thought I'd mention it because people often think that the theory must be wrong because light appears to go slower in transparent materials. Now to get back to relativity theory.
A simple explanation of special relativity
Imagine you are moving past me at 299,792,457 m/s, so that I would measure just 1 m/s difference between your speed and the speed of a light beam going in the same direction as you. By normal reasoning, I would expect you to measure the speed of the light beam as just 1 m/s faster than yourself. Instead the figure you get is 299,792,458 m/s. This appears to be an impossible situation.
Albert Einstein made the huge conceptual leap that solved this paradox. It had always been taken for granted that the universe marches to a single drum of time, so that a second is the same amount of time as measured by everyone. Also the metre was always thought to be the same length as measured by everyone. What if this was not the case? Speed is measured using distance and time. If I see that your ruler is shorter than mine and it takes many seconds on my clock before a second elapses on your clock, the speed that you measure (299,792,458 m/s) would be different to my estimate (1 m/s) because of these changes. This is what actually seems to happen. Your space and time distort relative to my viewpoint. As you go faster, I see your clock slow down and rulers (lined up in the direction you're moving) get shorter. You will always see your own clocks going at the correct rate and all your rulers will be the correct length, provided they remain stationary compared to you.
Light could not be used to measure the absolute speed of things in the universe relative to some absolutely stationary point in the universe. Einstein reasoned that there was no such sacred stationary speed. As long as you feel no forces on yourself, you have an equally valid view of the universe. You may regard yourself as stationary and I may regard myself as stationary, no matter what speed you are moving at relative to me. In the example above, you may regard yourself as stationary, and I am moving backwards at 299,792,457 m/s. Just as I see your ruler is far too short and your clock is going very slowly, you see my ruler as shorter than yours and my clock is going slower than yours. How can both these situations be true at the same time?
The thought experiment
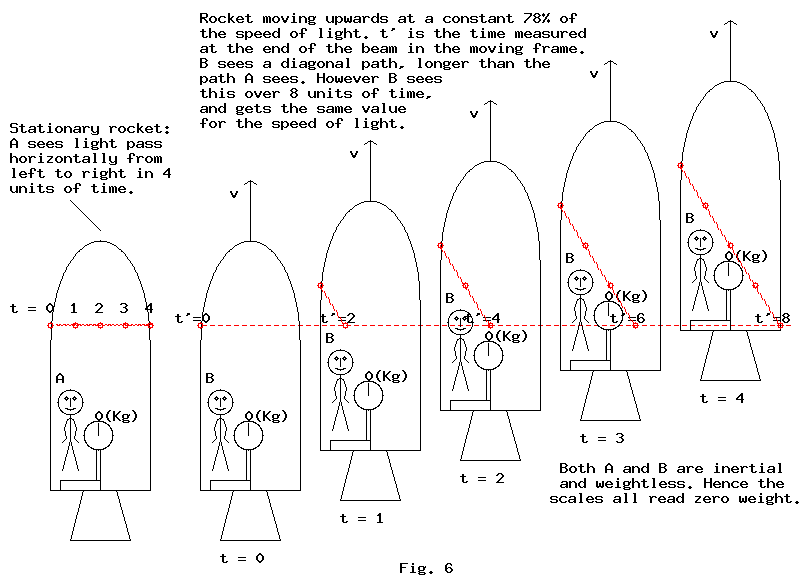
Imagine a flash lamp made up of many bulbs, all connected to timers. The timers are set to deliver a very short burst of electricity to the bulbs at the same time. When this time comes, all the bulbs flash simultaneously. The light is then collimated so that only rays perpendicular to the length of the flash lamp pass into the main experiment. Finally, a photographic film collects the light rays. The image on the film shows the situation simultaneously along the experiment.
A transparent ruler with embedded transparent clocks is placed between the collimator and the film. Fig. 1 shows this scenario and fig. 2 shows the outcome on the film. Since the ruler is stationary in this experiment, the result is unsurprising.

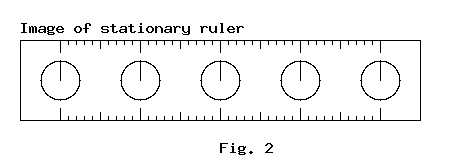
The image on the film shows all the clocks along the ruler reading the same time. This is only because the ruler is stationary relative to the flash lamp.
Simultaneity is relative
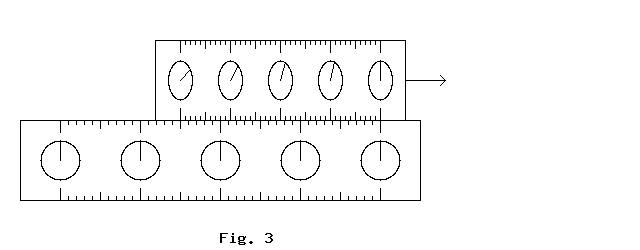
Providing all the clocks are reading the correct time, I will see my clocks reading the same time and you will see your clocks reading the same. But when I look at your clocks, I notice that the clock that is in front (in the direction of motion) is reading an earlier time than the clock at the back of your ruler. Conversely, when you look at my ruler, you see my clocks as reading different times. Again the leading clock reads the earlier time, though this is on the opposite end of the ruler because I am moving backward relative to you.
This difference in times explains how both see each other's ruler as shorter than their own. When I measure the length of your ruler, I mark each end at the same time, or simultaneously, as I measure it. However, you would notice that I measured the leading edge of the ruler earlier than the back. You would correctly guess that by the time I measured the back of your ruler, I would have seen it move towards the first measurement and so I would get a shorter length. By reversing this argument, the shorter length you measure for my ruler is explained in exactly the same way. But for each of us, the other's ruler really is shorter because we measured both ends at the same time as far as we are concerned.
Fig. 4. shows the situation as far as any observer on the moving ruler. Because this observer sees all the clocks on the moving ruler as reading the same time, the clocks on the stationary ruler read different times. So the moving observer will not see the flash bulbs all go off simulteously. The flash appears to move from the right to left.
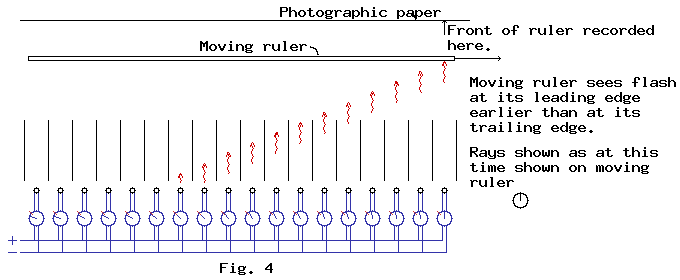
When I see two things happen at different places and at the same time, you will see them happen at different times. This is crucial to the explanation of the twins paradox.
The twins paradox
According to relativity theory, B can regard himself as stationary and A as moving at 87 per cent of the speed of light. From this point of view, A's clock is going slower than Bs. So A should be younger than B. But when they meet up which is the true situation?
In the above situation, when B and A meet up on earth where A is stationary, the viewpoint of A is the correct one.
So what's wrong with B's point of view? Remember that A doesn't see all the clocks moving with B reading the same time (as B does). If a clock attached to B moved past A as B was turning round to come back, A will not see the same time on that clock as the clock in B's cockpit. The cockpit clock is showing an earlier time whereas this clock shows a later time compared to A's clock. If we look at the situation as if B were stationary, he wouldn't notice A turn around until his cockpit clock read the same time as the clock passing A. By the time B sees A turn around, A's clock has advanced so that A is still older than B. This all assumes that B is seeing the final situation in terms of A's viewpoint. This is shown in fig. 5.
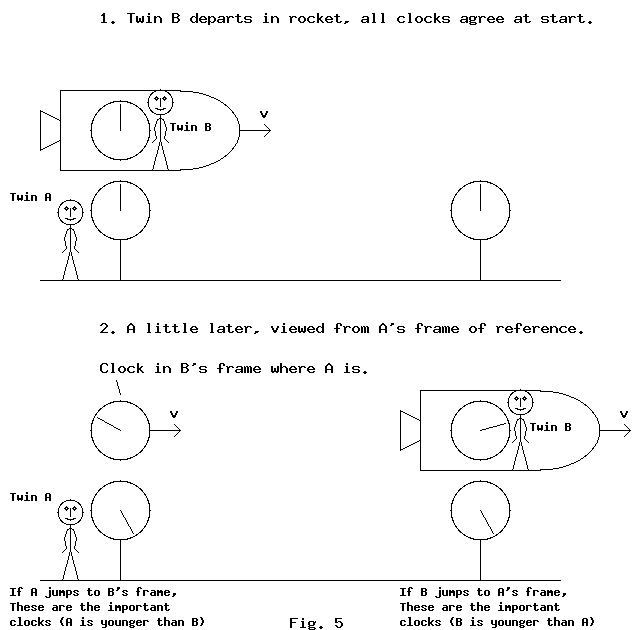
The idea of something not moving, or stationary, is relative. Nothing is absolutely stationary. The end result depends on what you decide is stationary. As long as everything finishes up stationary, the twin that was not stationary will always be younger. If A had ended up in B's spacecraft when they shake hands, A would be younger than B. From this point of view, "stationary" is B's velocity and A is the one that is doing all the movement. This may appear a bit mind bending but no fundamental conflicts are created at the end of the day. Relativity is all about points of view. We each see a picture that makes sense for ourself but it is not necessarily the same picture when viewed by someone else.
Time as a fourth dimension
Einstein noticed that his equations appeared very similar to equations for three dimensional motions except with an additional dimension. This dimension was a length, just like the space dimensions, but in a direction at right angles to the three space dimensions. In the equations the new length term is equal in size to the speed of light times the time difference. So one second in time represents a length of 299,792,458 metres.
The distance and the time interval between two events are both variable according to the relative velocity of the observer. But Einstein found a quantity that doesn't change. He called this quantity the "interval" between events. The interval combines the distance between the two events and the time interval between them in a particular way. When two observers are moving with respect to each other, they see two events from different viewpoints. The two observers see different distances between the events and different time intervals between them, but the interval is the same for both. The construction of the interval seems to imply a geometrical situation in which the length due to the time difference is at right angles to all the three components of the space diffence between the events.
Einstein saw that time really did seem to behave as if it were occupying a fourth dimension at right angles to the three dimensions of space. We can't picture such a dimension. Try putting three pens at right angles to each other. How could a fourth be placed so that it is at right angles to the all the others?
This fourth dimension has some strange properties. In space, we are used to going backwards and forwards in any of the three dimensions at will. Time only goes forwards. The second law of thermodynamics states this in terms of disorder (or entropy). It says that disorder in the universe always increases. It's easy to add together coloured inks (ordered) to make a mixture (disordered). Try to reverse the process and seperate the mixed ink back to the original inks.
Future, present and past
E=mc²
Suppose you throw a cup against the wall of your spacecraft, perpendicular to the motion of the spacecraft with enough momentum that it shatters on impact. I see that the cup moves the same distance as you see. But because I see time elapsing more slowly, I see the cup move more slowly and with less momentum. So it shouldn't shatter when it hits the wall. Einstein discovered that the only way to resolve this problem was to consider the mass of the cup. He realised that if the mass of the cup is relative and increases with the velocity of the spacecraft, the momentum that I measure could agree with the momentum you see. The cup is moving slower as I see it. But it is so much heavier that it has the same momentum as you measure and we both agree that the cup shatters on impact with the wall. This means that mass is a relative quantity. In your own stationary frame the mass is at rest and just has it's "rest mass". But a moving observer will see an increased mass.
Einstein arrived at a simple equation which showed how the mass of an object appeared to increase as it moved relative to you. When the object is not moving at all, the mass it has is called the "rest mass". He used the modified way of getting the momentum of an object to calculate the energy of a moving mass. This led to at a general energy formula where energy, E = mc². The "m" is the mass of the object and "c" is the speed of light. Einstein was surprised to find that if the velocity was set to zero, a residual energy value was left over. This energy is the E in E = mc², when m is just the rest mass. This residual energy is absolutely enormous! Just 1g of water (about a teaspoon) contains 90 trillion joules of energy. This would keep 10,000 light bulbs (100W) alight for nearly three years. Not bad for a teaspoon of water.
On facing this, Einstein had another profound idea. Mass is just a form of energy. Because energy can be converted from one form to another, so mass can be destroyed to release huge amounts of heat energy. Yes, it does provide the energy for nuclear bombs. But it also powers the sun and all the other stars. Even in these nuclear reactions only a tiny fraction of the mass of the atom is actually converted into energy. When matter meets antimatter, complete annihilation of the mass into heat can take place. Matter antimatter collisions make nuclear reactions seem puny.
The extreme situations
At very high speeds, the distortions go to extremes. I will see your long sleek spaceship become more and more stubby and your ship's clock go more slowly as you get closer to the speed of light. At 87 per cent of the speed of light, the length is halved, one second on your clock takes two on mine and you have doubled your mass. This factor 2 increases with velocity. At 94 per cent of the speed of light, the factor is 3, at 98 per cent it is 5, at 99.5 per cent it is 10, at 99.99995 per cent it is 100. If you could touch the speed of light, I would see your length shrink to nothing, your clock will stop and your mass would become infinite. Because of the mass increase, you will need an infinite amount of energy to touch the speed of light.
As a final note on special relativity, the speed of light appears to behave as if it were an infinite velocity but with a finite value. All measurements distort and conspire to make this finite speed so strange. Nobody knows why the speed of light happens to be 299,792,458 m/s. That's just what is measured.
Part 2. The general theory of relativity
Acceleration and gravity
Gravity is a force felt by everyone on earth. When an object falls, in a vacuum, in gravity, it accelerates towards the centre of the gravitational field. On the surface of the earth, the acceleration of all objects (in a vacuum) is nearly 10 m/s². That's about 0 to 60 mph in just over 2½ secs. Newton showed that the force of gravity is due to the presence of mass. It varies from place to place slightly because the earth bulges slightly and different rocks can affect the field because some rocks are heavier than others.
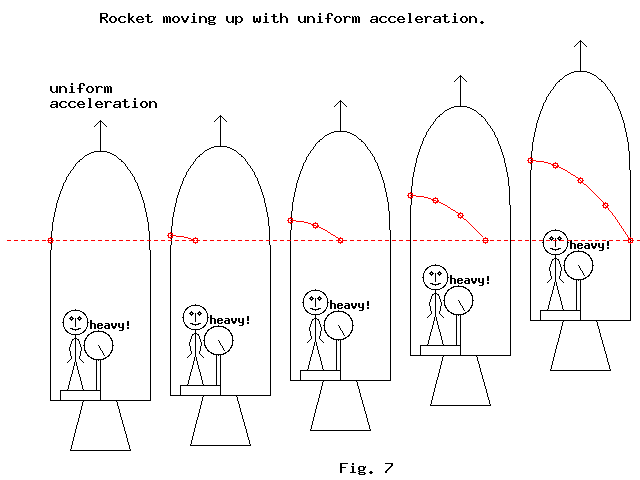
Now imagine you are in a spacecraft drifting in space (no gravity) with a "floor" on top of the rocket motor. With the motor off, you are weightless and the floor could just as well be a ceiling. When the rocket fires, you feel a force driving in the opposite direction to the acceleration of the craft. This makes you stick to the "floor". If the spacecraft accelerates at 10 m/s² and uses a very smooth rocket motor, you will feel as if you are in a normal gravity situation. You will be able to walk about the "floor" of the spacecraft as if on the surface of the earth. If you drop something, it will accelerate to the "floor" at 10 m/s² just as it would do on earth.
Now lets board up the windows of the spacecraft and play a little trick. We'll leave the spacecraft sticking vertically up on the launch pad so that you are still sitting on the "floor". We'll also arrange some heavy rocks to be placed under the launch pad in such a way that the force of gravity is perpendicular to the spacecraft floor everywhere the astronaut can measure the force. Is there any way that the astronaut could tell the difference between actual acceleration at 10 m/s² and standing still in the gravity field of earth?
Einstein's principle of general relativity states that gravitation and acceleration are equivalent. So the astronauts in the above situation should not be able to tell whether they are in a gravitational field or accelerating in an upward direction.
Curved space
If the spacecraft was accelerating, the path of the light beam will increase in slope as the velocity increased. In other words, the light appears to take a curved path. Fig. 7 shows a horizontal beam of light passing through a craft accelerating upwards from stationary. The craft is accelerating very rapidly to show such a noticeable bending. If the person in the craft is normal size, the light would take about 10 nanoseconds to get across the craft (final image of rocket). The rocket moves from stationary to a relativistic speed in about 10 nanoseconds. The person shown on the scales would weigh billions of tons!
If Einstein is right and you really can't tell the difference between gravity and acceleration then light beams should appear to bend if they pass through a gravity field. This formed a big test for Einsteins general theory of relativity. The bending of light by a gravitational force should become more significant for a big gravitational force in the same way that the bending of light becomes more exaggerated if acceleration is increased.
The strongest gravitational field observable in the solar system is the edge of the sun. During a total eclipse of the sun any stars in this region become visible from earth. In 1919, Sir Arthur Eddington observed a star that should have been totally hidden by the sun in a total eclipse. The angle of the deviation was in close agreement with the predicted bending of light that the sun's gravity would exert on the path of the light from the star. This was a major experimental vindication of the general theory of relativity.
The implications of this are very strange. When we consider the very special properties of the speed of light in special relativity and the nature of light in accelerating and gravitational fields, it appears as if the shortest path between two points is only straight when taken from a certain viewpoint. From another viewpoint, the shortest path is a curve and what you perceive to be straight is actually longer. Remember trying to fit three dimensions with pens at right angles to each other to represent the three dimensions of space? In the general theory of relativity, the angles between the pens differ according to how you view the situation. So space and time not only distort in size but in direction as well. This is the basis for the idea of curved space-time.
Gravity (or acceleration) is relative
However if you falling freely in England and feel weightless in the lift as the cable snaps, it may comfort you to know that, relative to yourself, there is no gravitational force acting on you. The gravitational force in Australia, is twice as strong, relative to you, as that measured by a stationary observer (someone who didn't get in the lift). When you are in free fall, light travels in straight lines in all directions and all the dimensions are at right angles to each other, as if you were in back in the simple conditions for special relativity (no forces acting on you).
An "inertial" view is effectively the viewpoint of someone who feels weightless. This can be someone travelling at a constant velocity in no force fields (special relativity) or someone falling in a lift. If someone is in an inertial situation, the world appears a lot simpler. Straight lines really are straight and the dimensions really do meet up at right angles. This is an essential point about relativity theory. It is only to observers, who do not share your "frame of reference", that distortions appear.
Einstein found a single mathematical formulation that allowed any situation to be observed relative to any other situation. Because straight lines can become curved and the dimensions don't always meet up at right angles for different observers, the complete mathematical description of this is extremely difficult, even for mathematicians.
Black holes
However as the object collapses the gravitational force around the edge increases. Someone outside the object sees light passing the edge curves as space-time itself distorts around the object. At a certain point called the "event horizon", light beams are curved to such an extent that they cannot actually escape. After this point, we cannot see the object itself. Light rays cannot escape from the black hole to reach our eyes. At the event horizon, space and time itself go to the extreme limit of relativity theory.
If you stand well outside the black hole and throw a clock into towards the hole. As the clock drifts away from you it will start slowing down. This continues until the clock reaches the event horizon and stops completely. Time itself stops at the event horizon.
But you may find it difficult to read the time on the clock because it will start to stretch out. This process has been called "stringification" by some. Just as time goes to the extreme of stopping completely at the event horizon, space also goes to extremes. At the event horizon, any object of finite size will stretch around the entire surface as if the surface area is zero.
If you decide to fall towards the black hole and somehow survive the nightmarish tidal forces on you, you will reach the event horizon in a finite time. You will see the outside universe go through an infinite amount of time as you touch the event horizon.
Within the event horizon of a black hole, relativity predicts that there is still a geometry, but it is "incomplete". Directions only exist towards the singularity. The singularity stretches away from you to infinity and it takes an infinite amount of time to actually reach the singularity. The strange thing is, once inside the event horizon, you can never communicate with anything outside the event horizon.
Black holes were originally considered theoretical oddities that wouldn't actually be found. However, astronomers have observed strange behaviour that is consistent with the theories of black holes. Although the hole itself cannot be directly detected, distortions of light close to a black hole would create strange "gravitational lens" effects. Stephen Hawking has also shown how matter falling into a black hole will emit radiation. Both these effects have been observed. Astronomers now believe that gigantic black holes sit at the centre of galaxies.